Centrality Measures Update
Source:vignettes/centrality_maesures_update.Rmd
centrality_maesures_update.RmdIntroduction
The new release of ConnectR provides some aesthetic upgrades and built-in calculation of node centrality measures. These upgrades provide powerful tools to measure networks with, and give users more flexibility of approach.
With great power comes great responsibility! It is expected, for
example, that by the time the user comes to create a centrality network
he/she knows whether their network should be treated as directed or
undirected, and what this choice means for each respective centrality
measure. For example, if a network is directed and acyclic (no path from
one node to all others) then Eigenvector Centrality is not
defined and will = 0 in all cases. In undirected networks,
degree_in and degree_out collapse into
degree - or the total number of edges associated with a
node.
For a primer on centrality measures for networks, see: Wikipedia Centrality Measures
Retweet networks with Centrality Measures
Get the data
Let’s load the libraries we will need and get some data:
library(ConnectR)
library(tidyverse)
rts <- retweet_example %>%
janitor::clean_names()Calculate Centrality - Directed Network
The first major change to the workflow is the
calculate_centrality function. The function takes in a
dataset, asks for a from and to variable, asks
whether the network should be treated as directed, and what
the damping factor should be for the PageRank
algorithm.
A quick word on directed vs undirected networks. Loosely speaking, a directed network is a network in which the edges - or the connection between nodes - are asymmetrical, i.e. if User A retweets user B, but user B does not retweet user A, there is a path from A –> B but there is not a path from B –> A. A retweet network is therefore directed, as is a mention network.
An undirected network is a network where the edges are symmetrical, i.e. if A is friends with B on Facebook, then B is also friends with A. Therefore, the edge that connects them creates a path from A – > B and a path from B –> A.
Notice a warning about ‘nobigint’ which is an argument in the calculation for betweenness - notice it and then ignore it :).
(rt_centrality <- rts %>%
calculate_centrality(from = sender, to = original_author, directed = TRUE))
#> Warning in betweenness(graph = graph, v = V(graph), directed = directed, :
#> 'nobigint' is deprecated since igraph 1.3 and will be removed in igraph 1.4
#> Warning in eigen_centrality(graph = .G(), directed = directed, scale = scale, :
#> At core/centrality/centrality_other.c:329 : graph is directed and acyclic;
#> eigenvector centralities will be zeros.
#> $edges
#> # A tibble: 921 × 13
#> from to n_retweets degree_in_to degree_out_to betweenness_to page_rank_to
#> <chr> <chr> <int> <dbl> <dbl> <dbl> <dbl>
#> 1 "–ë–… Rona… 1 245 0 0 0.135
#> 2 "–í–… Rona… 1 245 0 0 0.135
#> 3 "–ü–… Rona… 1 245 0 0 0.135
#> 4 "–û–… Rona… 1 245 0 0 0.135
#> 5 "‚òÅ… mark… 1 60 0 0 0.0333
#> 6 "(A.… Rona… 1 245 0 0 0.135
#> 7 "‡§Ö… stpi… 1 130 0 0 0.0581
#> 8 "‡§Ö… Omka… 1 123 0 0 0.0539
#> 9 "‡§Ö… stpi… 1 130 0 0 0.0581
#> 10 "‡§µ… mark… 1 60 0 0 0.0333
#> # … with 911 more rows, and 6 more variables: eigen_to <dbl>,
#> # degree_in_from <dbl>, degree_out_from <dbl>, betweenness_from <dbl>,
#> # page_rank_from <dbl>, eigen_from <dbl>
#>
#> $user_stats
#> # A tibble: 879 × 8
#> name degree_in degree_out betweenness page_rank eigen user_retweets_o…
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <int>
#> 1 –ë–æ–≥–¥–∞… 0 1 0 0.000656 0 1
#> 2 Ronald_van… 245 0 0 0.135 0 NA
#> 3 –í–ª–∞–¥–∏… 0 1 0 0.000656 0 1
#> 4 –ü–∞–≤–µ–ª… 0 1 0 0.000656 0 1
#> 5 –û–ª–µ–≥ –… 0 1 0 0.000656 0 1
#> 6 ‚òÅÔ∏èStev… 0 1 0 0.000656 0 1
#> 7 markrussin… 60 0 0 0.0333 0 NA
#> 8 (A.R.A.)® 0 1 0 0.000656 0 1
#> 9 ‡§Ö‡§Æ‡§® … 0 1 0 0.000656 0 1
#> 10 stpiindia 130 0 0 0.0581 0 NA
#> # … with 869 more rows, and 1 more variable: user_gets_retweeted <int>The function returns a list of 2 items - edges,
user_stats. edges will be plucked and passed
on to the viz_centrality_network() or
create_supercluster() functions, user_stats is
a data frame providing author-level metrics, useful for creating a
custom score or for general exploration.
Exploring Edges
If we purrr::pluck() our edges, we can take a closer
look at what the calculate_centrality() function has done
for us:
edges <- rt_centrality %>% pluck('edges')
glimpse(edges)
#> Rows: 921
#> Columns: 13
#> $ from <chr> "–ë–æ–≥–¥–∞–Ω –ó—É–±–µ—Ü", "–í–ª–∞–¥–∏–º–∏—Ä –ò–≤–∞–Ω…
#> $ to <chr> "Ronald_vanLoon", "Ronald_vanLoon", "Ronald_vanLoon",…
#> $ n_retweets <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
#> $ degree_in_to <dbl> 245, 245, 245, 245, 60, 245, 130, 123, 130, 60, 123, …
#> $ degree_out_to <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
#> $ betweenness_to <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
#> $ page_rank_to <dbl> 0.1352045763, 0.1352045763, 0.1352045763, 0.135204576…
#> $ eigen_to <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
#> $ degree_in_from <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
#> $ degree_out_from <dbl> 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
#> $ betweenness_from <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
#> $ page_rank_from <dbl> 0.0006564695, 0.0006564695, 0.0006564695, 0.000656469…
#> $ eigen_from <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…We now have columns named from and to which
tell us the direction of the interaction, i.e. from
retweeted to. n_retweets tells us how many
times from has retweeted to in our dataset,
and we have centrality measures for to and centrality
measures for from. This is a potentially confusing output,
so why have we done it this way?
A user may want to reduce the size of the network for a variety of
reasons, and it is important to be able to use centrality metrics to
filter on from and to.
So what do our other new columns mean?
degree_in_x = the number of times a user was retweeted
in total
degree_out_x= the number of times a user retweeted
others in total
betweenness_x = the number of shortest paths between two
other nodes a user figures in
page_rank_to = roughly the proportion of times a user
travelling around the network at random would end up at a node.
eigen_x = the Eigenvector Centrality score for a node -
roughly speaking this estimates a node’s influence by considering the
influence of its connections too. The highest scoring node will always =
1.
Advanced - Joining other features from dataset
We can add variables such as followers back to our
dataset if we’re going to want to use them as size or colour when we
visualise the network.Ot’s important to note that in the case of
followers, we have information on the from
variable - i.e. the person who is retweeting, not the person who is
being retweeted.
We can use our new followers variable to get the mean
number of followers interacting with each original_author like so:
tmp_join <- rts %>% select(sender, followers)
edges <- edges %>% left_join(tmp_join, by = c("from" = "sender"))
edges <- edges %>%
group_by(to) %>%
#Get the mean of the followers who have retweeted a user.
mutate(mean_followers = mean(followers, na.rm = TRUE)) %>%
ungroup()
rm(tmp_join)It’s at this point that the user should determine which metrics will figure as node size and node colour. Again, the onus is very much on the user to interpret the statistics they now find themselves with. Given the complexity of network analysis, there is not currently an algorithmic approach to deciding which metrics should be focused on - it is dependent on the type of network being analysed, and the information the user is trying to convey.
It’s a good idea to use standard data exploration/visualisation techniques to investigate which statistics may be useful for size and colour. You can create histograms, boxplots, and other standard charts for each variable, but for now we will take a quick look at some summary statistics.
summary(edges)
#> from to n_retweets degree_in_to
#> Length:7186 Length:7186 Min. : 1.000 Min. : 1.00
#> Class :character Class :character 1st Qu.: 1.000 1st Qu.: 1.00
#> Mode :character Mode :character Median : 1.000 Median : 2.00
#> Mean : 1.321 Mean : 24.01
#> 3rd Qu.: 1.000 3rd Qu.: 7.00
#> Max. :15.000 Max. :245.00
#> degree_out_to betweenness_to page_rank_to eigen_to degree_in_from
#> Min. :0 Min. :0 Min. :0.0006648 Min. :0 Min. :0
#> 1st Qu.:0 1st Qu.:0 1st Qu.:0.0006648 1st Qu.:0 1st Qu.:0
#> Median :0 Median :0 Median :0.0012228 Median :0 Median :0
#> Mean :0 Mean :0 Mean :0.0122872 Mean :0 Mean :0
#> 3rd Qu.:0 3rd Qu.:0 3rd Qu.:0.0031758 3rd Qu.:0 3rd Qu.:0
#> Max. :0 Max. :0 Max. :0.1352046 Max. :0 Max. :0
#> degree_out_from betweenness_from page_rank_from eigen_from
#> Min. : 1.00 Min. :0 Min. :0.0006565 Min. :0
#> 1st Qu.:67.00 1st Qu.:0 1st Qu.:0.0006565 1st Qu.:0
#> Median :67.00 Median :0 Median :0.0006565 Median :0
#> Mean :55.95 Mean :0 Mean :0.0006565 Mean :0
#> 3rd Qu.:67.00 3rd Qu.:0 3rd Qu.:0.0006565 3rd Qu.:0
#> Max. :67.00 Max. :0 Max. :0.0006565 Max. :0
#> followers mean_followers
#> Min. : 0 Min. : 4
#> 1st Qu.: 2053 1st Qu.: 2569
#> Median : 2639 Median : 2597
#> Mean : 4039 Mean : 4039
#> 3rd Qu.: 2911 3rd Qu.: 2609
#> Max. :643702 Max. :643702Visualise Centrality Network
Static
Looking at our selection of edges, it would appear that degree_in_to (number of retweets a user has received) and page_rank_to would suit a first visualisation; these two are a good guide for the type of directed networks we encounter.
we will make a static, directed graph, where we label any node which is in the top 10% of our size or colour variables:
edges %>%
viz_centrality_network(colour = page_rank_to, size = degree_in_to, directed = TRUE, type = "static", label_prop = 0.1)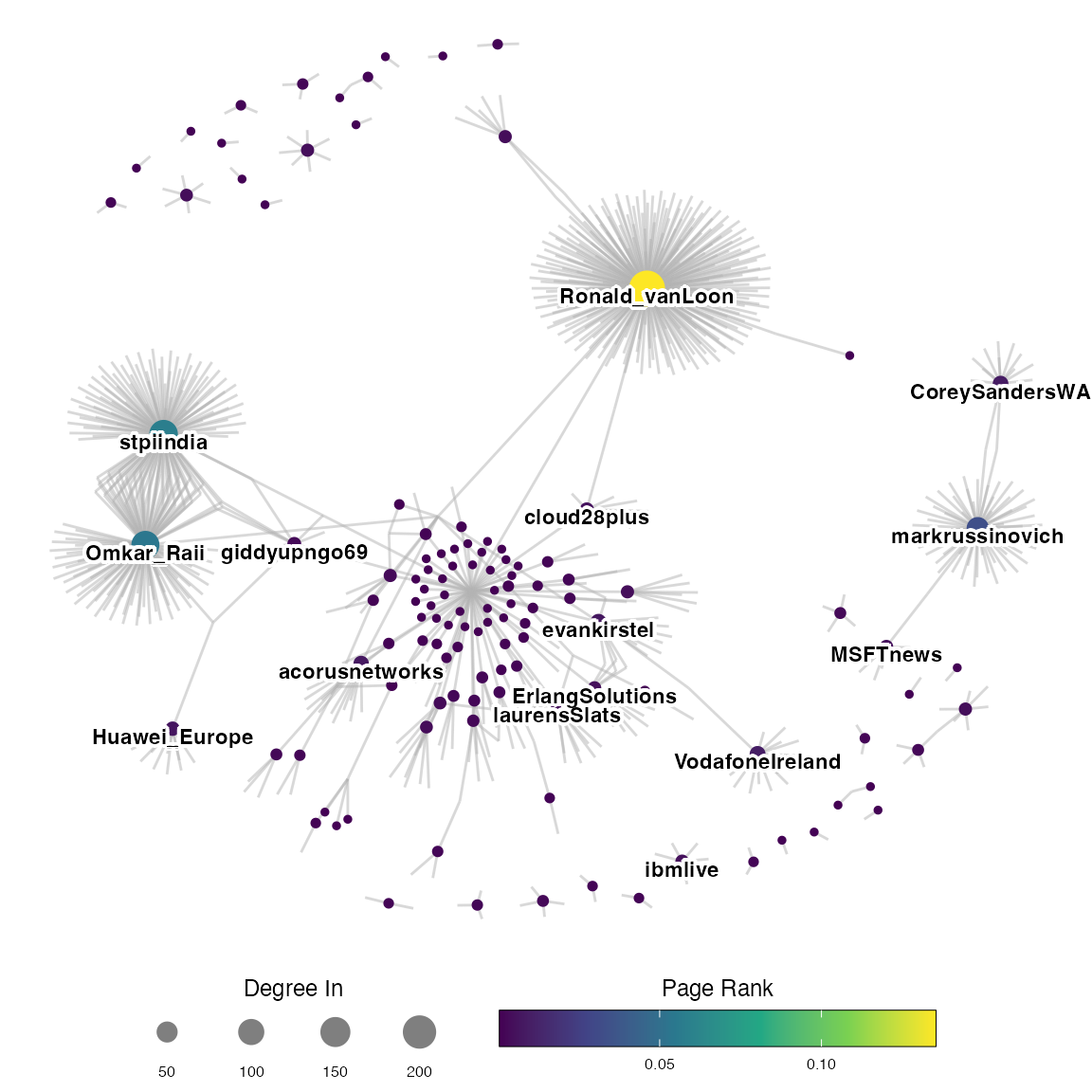
Interactive
Now we will create an interactive network, we will use the same size/colour variables as we did for the static network:
edges %>%
viz_centrality_network(colour = page_rank_to, size = degree_in_to, directed = TRUE, type = "interactive", physics = TRUE, width = "700px", height = "600px")Notice that the nodes are flying around, as if in a mini-universe of interacting objects - depending on how long it took you to get to this stage as the movement will cease eventually - this is because we have set physics to TRUE. Sometimes without physics our interactive graphs will not settle on an appropriate layout. If you turn it off, you may sometimes find nodes clustered tightly and not ‘spreading out’.
we will also add a title and some explanatory text to the subtitle.
See ?visNetwork::visNetwork() for additional arguments.
edges %>%
viz_centrality_network(colour = page_rank_to, size = degree_in_to, directed = TRUE, type = "interactive", physics = FALSE, main = "ConnectR Centrality Release Interactive Plot",
submain = "We can see that Ronald_vanLoon is an influential node in the network, as well as Omkar_Raii & stpiindia", width = "700px", height = "600px")Undirected Network
Where possible, it is generally not advised to convert a directed network to an undirected network. However, for practical reasons modelling a directed network as an undirected network can be useful - as long as the user understands what information was lost in the process.
If converting a retweet network to an undirected network, we lose
information on who interacted with whom; so all we know is that there
was an interaction between two users. However, we gain access to
Eigenvector Centrality as a measure of centrality, which
will take into account not just a node’s number of connections, but how
influential those connections are themselves. We can also approximate
betweenness for users who have not retweeted other users.
(directed <- rts %>% calculate_centrality(from = sender, to = original_author, directed = FALSE))
#> Warning in betweenness(graph = graph, v = V(graph), directed = directed, :
#> 'nobigint' is deprecated since igraph 1.3 and will be removed in igraph 1.4
#> $edges
#> # A tibble: 921 × 11
#> from to n_retweets degree_to betweenness_to eigen_to page_rank_to
#> <chr> <chr> <int> <dbl> <dbl> <dbl> <dbl>
#> 1 "–ë–æ–≥–¥–∞–… Rona… 1 245 139446. 1 0.127
#> 2 "–í–ª–∞–¥–∏–… Rona… 1 245 139446. 1 0.127
#> 3 "–ü–∞–≤–µ–ª … Rona… 1 245 139446. 1 0.127
#> 4 "–û–ª–µ–≥ –ò… Rona… 1 245 139446. 1 0.127
#> 5 "‚òÅÔ∏èSteve… mark… 1 60 3232. 0 0.0313
#> 6 "(A.R.A.)¬Æ" Rona… 1 245 139446. 1 0.127
#> 7 "‡§Ö‡§Æ‡§® ‡… stpi… 1 130 74475. 0.0198 0.0544
#> 8 "‡§Ö‡§Æ‡•ã‡§… Omka… 1 123 57869. 0.0170 0.0509
#> 9 "‡§Ö‡§Æ‡•ã‡§… stpi… 1 130 74475. 0.0198 0.0544
#> 10 "‡§µ‡§ø‡§ï‡•… mark… 1 60 3232. 0 0.0313
#> # … with 911 more rows, and 4 more variables: degree_from <dbl>,
#> # betweenness_from <dbl>, eigen_from <dbl>, page_rank_from <dbl>
#>
#> $user_stats
#> # A tibble: 879 × 7
#> name degree betweenness eigen page_rank user_retweets_o… user_gets_retwe…
#> <chr> <dbl> <dbl> <dbl> <dbl> <int> <int>
#> 1 –ë–æ–… 1 0 0.0638 0.000610 1 NA
#> 2 Ronal… 245 139446. 1 0.127 NA 254
#> 3 –í–ª–… 1 0 0.0638 0.000610 1 NA
#> 4 –ü–∞–… 1 0 0.0638 0.000610 1 NA
#> 5 –û–ª–… 1 0 0.0638 0.000610 1 NA
#> 6 ‚òÅÔ∏… 1 0 0 0.000614 1 NA
#> 7 markr… 60 3232. 0 0.0313 NA 60
#> 8 (A.R.… 1 0 0.0638 0.000610 1 NA
#> 9 ‡§Ö‡§… 1 0 0.00126 0.000526 1 NA
#> 10 stpii… 130 74475. 0.0198 0.0544 NA 133
#> # … with 869 more rowsNotice that we picked out Ronald_vanLoon as an influential user in our directed network - his betweenness has gone from 0 in the directed network to 139,446 in the undirected. Why?
In our directed network there was no path out from his node because he had not retweeted anyone, meaning he did not figure in any shortest paths - anyone attempting to travel through the network would get stuck.
We also have an Eigenvector Centrality score.
Also notice that we do not have degree_in and degree_out columns - this is because in undirected networks degree is the total number of edges that attach to each node.
Create a supercluster
Social media networks are often large and disconnected - disconnected meaning there are many unconnected subcommunities, or subclusters. Sometimes we want to focus specifically on the largest connected cluster of nodes. We can use the create_supercluster function to do so.
First we calculate_centrality(), then we pluck the edges
and feed them into the create_supercluster() function.
rt_supercluster <- rts %>% calculate_centrality(from = sender, to = original_author, directed = TRUE)
#> Warning in betweenness(graph = graph, v = V(graph), directed = directed, :
#> 'nobigint' is deprecated since igraph 1.3 and will be removed in igraph 1.4
#> Warning in eigen_centrality(graph = .G(), directed = directed, scale = scale, :
#> At core/centrality/centrality_other.c:329 : graph is directed and acyclic;
#> eigenvector centralities will be zeros.
rt_supercluster <- rt_supercluster %>%
pluck('edges') %>%
create_supercluster(directed = TRUE)
#> Warning: The `x` argument of `as_tibble.matrix()` must have unique column names if `.name_repair` is omitted as of tibble 2.0.0.
#> Using compatibility `.name_repair`.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.
#> Warning in betweenness(graph = graph, v = V(graph), directed = directed, :
#> 'nobigint' is deprecated since igraph 1.3 and will be removed in igraph 1.4
#> Warning in eigen_centrality(graph = .G(), directed = directed, scale = scale, :
#> At core/centrality/centrality_other.c:329 : graph is directed and acyclic;
#> eigenvector centralities will be zeros.Visualise supercluster
now let’s visualise:
rt_supercluster %>%
viz_centrality_network(colour = page_rank_to, size = degree_in_to)Mention Network
To make a mention network with centrality measures, we will first extract mentions from a text variable and then we will calculate centrality and visualise.
One thing to note is that there will tend to be many more mentions per post than retweets as some posts mention tens of accounts. When added to the fact that a user can be mentioned without tweeting beforehand - unlike in the retweet network, where a tweet is a necessary requirement to being retweeted - this can make it difficult for graph-solving algorithms to correctly place nodes. Another way of thinking about this is that the universe of possible mentions is much larger than the universe of possible retweets.
mentions <- mention_example %>%
janitor::clean_names()
mentions <- extract_mentions(mentions, author_variable = screen_name, text_variable = text)
mentions_centrality <- mentions %>%
calculate_centrality(from = screen_name, to = mentions, directed = TRUE)
#> Warning in betweenness(graph = graph, v = V(graph), directed = directed, :
#> 'nobigint' is deprecated since igraph 1.3 and will be removed in igraph 1.4
#> Warning in eigen_centrality(graph = .G(), directed = directed, scale = scale, :
#> At core/centrality/centrality_other.c:329 : graph is directed and acyclic;
#> eigenvector centralities will be zeros.Now we should inspect the network to determine what our size and colour variables should be. we will pluck the user stats data frame first, and arrange it by degree_in - or the number of times a user was mentioned.
mentions_centrality %>% purrr::pluck('user_stats') %>%
arrange(desc(degree_in))
#> # A tibble: 1,301 × 8
#> name degree_in degree_out betweenness page_rank eigen user_retweets_o…
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <int>
#> 1 nytimes 7 0 0 0.00113 0 NA
#> 2 WSJ 5 0 0 0.000899 0 NA
#> 3 amazon 4 0 0 0.000812 0 NA
#> 4 realDonald… 4 0 0 0.000896 0 NA
#> 5 YouTube 4 0 0 0.000938 0 NA
#> 6 elonmusk 4 0 0 0.000802 0 NA
#> 7 Google 4 0 0 0.000860 0 NA
#> 8 Facebook 3 0 0 0.000831 0 NA
#> 9 washington… 3 0 0 0.000828 0 NA
#> 10 Forbes 3 0 0 0.000795 0 NA
#> # … with 1,291 more rows, and 1 more variable: user_gets_retweeted <int>We can see that all of our top 10 most-mentioned accounts have 0 degree_out - which means they have not mentioned anyone else, which given that our network is directed, means all of these accounts are also 0 for betweenness. We hinted at some of the differences between a mention network and a retweet network, here we see another corollary of the universe of mentions being much larger than the universe of retweets - our mention network is sparser.
It looks like degree_in and page_rank will be the optimal colour and size variables here:
mentions_centrality %>%
pluck('edges') %>%
viz_mention_centrality_network(size = degree_in_to, colour = page_rank_to, type = "static", label_prop = 0.05, physics = TRUE)
#> Warning: Removed 1176 rows containing missing values (geom_point).
#> Warning: Removed 1256 rows containing missing values (geom_shadow_text).
We can create an interactive visualisation similarly to how we did for our retweet networks. It’s recommended to allow physics when creating an intereactive mention network, as without them it is often difficult for our graph-solving algorithm to arrange our network in a pleasing manner.
mentions_centrality %>%
pluck('edges') %>%
viz_mention_centrality_network(size = degree_in_to, colour = page_rank_to, type = "interactive", label_prop = 0.01, physics = TRUE)Potential error message(s)
“Error in rlang::ensym(): ! Can’t convert to a
symbol.”
This probably means that you have not specified a size or colour variable, and you need to!